第24次CCFCSP解题报告

7.5k字   |   预计阅读时长: 36min
阅读量: 次   

本次报告撰写人：WilliamZH
题目：202112，第24次CCFCSP
使用语言：C++

题目 1：序列查询

题目描述：

$A$ 是一个由 $n+1$ 个 $[0,N)$ 范围内整数组成的序列，递增，默认 $A[0]=0$。
定义查询 $f(x)$ 为：序列 $A$ 中 $≤x$ 的整数里最大的数的下标。
令 $sum(A)$ 表示 $f(0)$ 到 $f(N-1)$ 的总和。
对于给定的序列 $A$，求 $sum(A)$。
$1≤n≤200，n<N≤10⁷$

题解：

解法一：

$i$ 遍历 $0∼N-1$，再遍历序列 $A$，记最大值 $j$ 为下一次遍历起点。

时间复杂度$O(n+N)$，空间复杂度$O(n)$，期望得分100

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
using namespace std;

int main()
{
    int n, N, A[201] = { 0 };
    cin >> n >> N;
    for (int i = 1; i <= n; i++)
        cin >> A[i];
    int ans = 0;
    int flag = 0;
    for (int i = 0; i < N; i++) {
        int j = flag;
        while (A[j] <= i && j <= n)
            j++;
        ans += j - 1;
        flag = j - 1;
    }
    cout << ans << endl;
    return 0;
}

解法二：

进一步优化效率。
若存在区间 $[i,j)$ 满足 $f(i)=f(i+1)=…=f(j-1)$，使用乘法运算 $f(i)×(j-i)$ 代替逐个相加。

时间复杂度$O(n)$，空间复杂度不变，期望得分100

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<iostream>
using namespace std;
int main()
{
    int n, N, A[201] = { 0 }, ans = 0;
    cin >> n >> N;
    for (int i = 1; i <= n; i++) {
        cin >> A[i];
        ans = ans + (A[i] - A[i - 1]) * (i - 1);
    }
    ans += (N - A[n]) * n;
    cout << ans << endl;
    return 0;
}

题目 2：序列查询新解

题目描述：

$A$ 是一个由 $n+1$ 个 $[0,N)$ 范围内整数组成的序列，递增，默认 $A[0]=0$。
定义查询 $f(x)$ 为：序列 $A$ 中 $≤x$ 的整数里最大的数的下标。
如果 $A1,A2,⋯,An$ 均匀分布在 $(0,N)$ 的区间，那么就可以估算出：
$$f(x)≈\frac{(n-1)∙x}{N}$$
定义比例系数 $r=⌊\frac{N}{n+1}⌋$，用 $g(x)=⌊\frac{x}{r}⌋$ 表示估算出的 $f(x)$ 的大小。
用 $∣g(x)-f(x)∣$ 表示询问 $x$ 时的误差。
计算 $$ error(A)=\sum∣g(0)-f(0)∣+…+∣g(N-1)-f(N-1)∣$$
$1≤n≤10^5，n<N≤10^9$

题解：

解法一：

该解法同题一的解法一，计算 $f(x)$ 的同时计算每一个 $g(x)$。
但由于 $n$ 的范围增大，时间复杂度较高，导致超时。

时间复杂度$O(n+N)$，空间复杂度$O(n)$，期望得分70

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
#include<cmath>

using namespace std;

int main()
{
    int n, N, A[100001] = { 0 };
    cin >> n >> N;
    for (int i = 1; i <= n; i++)
        cin >> A[i];
    int r = N / (n + 1);
    int ans = 0;
    int flag = 0;
    for (int i = 0; i < N; i++) {
        int j = flag;
        while (A[j] <= i && j <= n)
            j++;
        ans += abs(j - 1 - i / r);
        flag = j - 1;
    }
    cout << ans << endl;
    return 0;
}

解法二：

优化方法类似题一的解法二，在对 $f(x)$ 分组的同时，对相同的 $f(x)$ 内部再对 $g(x)$ 分组。
则该区间内的和为 $abs(f(i)-g(i))*gNum$，$gNum$ 表示该区间 $g(j)$ 的个数。

时间复杂度$O(n)$，空间复杂度不变，期望得分100

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
#include<cmath>
using namespace std;
int A[100001];
int main()
{
    ios::sync_with_stdio(false);
    int n, N;
    cin >> n >> N;
    int r = N / (n + 1);
    for(int i = 1; i <= n; i++)
        cin >> A[i];
    A[n + 1] = N;
    long long ans = 0;
    int gnum = 0;
    for (int i = 0; i <= n; i++)
        for (int j = A[i]; j < A[i + 1]; j += (gnum - j)) {
            gnum = (j / r + 1) * r;
            if (gnum > A[i + 1])
                gnum = A[i + 1];
            ans += abs(j / r - i) * (gnum - j);
        }
    cout << ans << "\n";
    return 0;
}

题目 3：登机牌条码

题目描述：

  1. 对于输入的被编码的数据，按照给定的表进行编码。
  2. 数据码字由以下数据按顺序拼接而成（如图所示）：
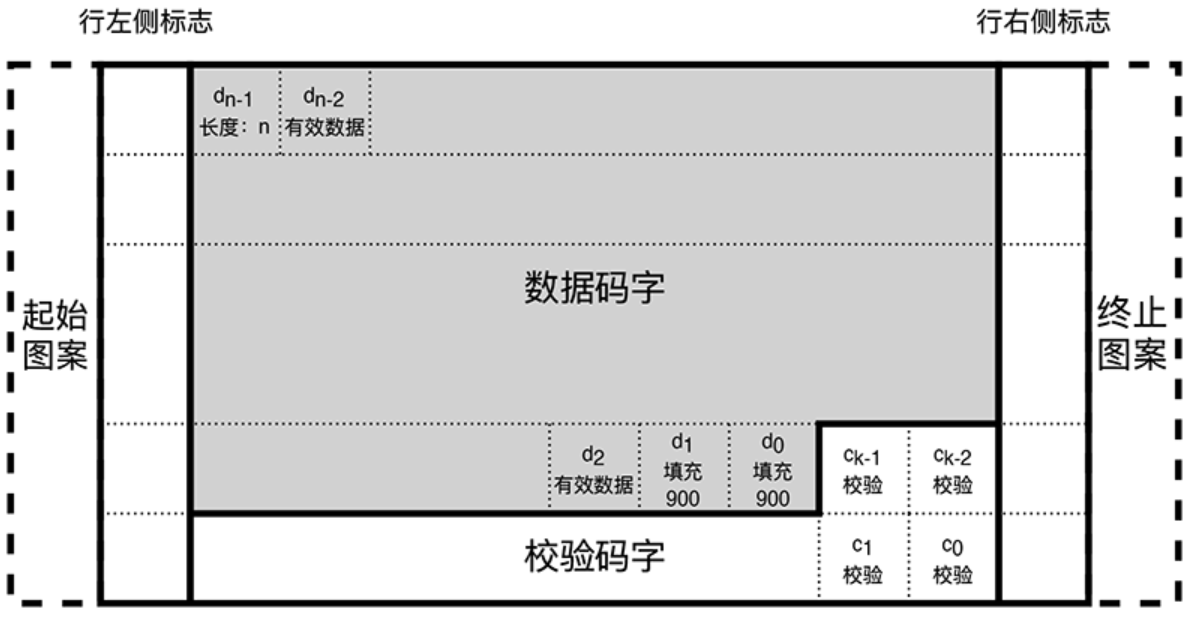
  • 一个长度码字，表示全部数据码字的个数 $n$，包括该长度码字、有效数据码字、填充码字；
  • 若干有效数据码字，是此前计算的码字序列；
  • 零个或多个由重复的 $900$ 组成的填充码字，使得包括校验码字在内的码字总数恰能被有效数据区的行宽度整除。
  1. 校验码字按照如下方式计算：
    取 $k$ 次多项式 $g(x)=(x−3)(x−3^2)…(x−3^k)$, $(n−1)$ 次多项式 $d(x)$，找到多项式 $q(x)$ 和不超过 $(k−1)$ 次的多项式 $r(x)$，使得 $x^kd(x)≡q(x)g(x)−r(x)$。
    那么多项式 $r(x)$ 中 $x$ 的 $i$ 次项系数对 $929$ 取模后（取正值）的数字即为校验码字 $c_i$。
    给定被编码的数据，计算出需要填入有效数据区的码字序列。被处理的数据中只含有大写字母、小写字母和数字。

题解：

解法一：

  1. 首先处理字符串，计算对应的数字：
    用数组 $a$ 存储每一位数字，用 $pre$ 存储上一个字符的处理状态；数组最后一位下标若为偶数，则补充一个 $29$ 。
  2. 计算码字：
    用数组 $d$ 存储有效数据的码字，有效数据的个数用 $dnum$ 存储。
  3. 计算校验码字个数：
    $s==-1$ 时，$k=0$；否则 $k=pow(2,s+1)$。
  4. 计算填充码字：
    总长度 $sum = dnum + 1 + k$，判断是否可被 $w$整除，以及填充多少个 $900$，同时 $dnum$ 相应增加。

不考虑校验码字，至此即可得40分。

解法二：

接着解法一的四步，计算校验码字。
5. 计算校验码字：

  • 预处理公式：等式两边同时对 $g(x)$ 取余，则 $x^kd(x) mod g(x) ≡ -r(x) mod g(x)$。即求 $x^k d(x) mod g(x)$ 后取反。
  • 避免数据溢出，需在计算过程中取模。
  • 计算 $g(x)$ 时考虑到每一次多项式乘以的因子都是 $(x−a)$ 的格式， 所以可以把 $A*(x−a)$的多项式相乘转化为 $xA−aA$ 的格式。 $x*A$ 可以通过整体移项实现；在移项后，原本在 $x_i$ 的系数成为 $x_{i+1}$ 的系数。
  • 首先, $t$ 被初始化为 $-3$，然后 $g[0]$ 被初始化为 $1$，表示 $g(x)$ 中 $x^0$ 的系数为 $1$。
    然后，外层循环 $i$ 从 $1$ 到 $k$，每次循环将 $t$ 乘以 $3$，表示将多项式中的 $x-3$，$x-3^2$ 等因子依次处理。内层循环 $j$ 从 $i - 1$ 到 $0$，对于每个 $j$，使用递推的方法计算 $g(x)$ 中 $x^j$ 的系数。具体来说，根据多项式的乘法规则，$x^j$ 可以由 $x^{j-1}$ 和 $x^j$ 两项乘以 $-3^i$ 而得到，即：
    $$
    x^j = (x^{j-1} \cdot (-3^i)) + (x^j \cdot (-3^i))
    $$
    这个式子中，$x^{j-1}$ 代表 $g(x)$ 中 $(x - 3^{i-1})$ 的贡献，而 $x^j$ 代表 $g(x)$ 中 $(x - 3^i)$ 的贡献。因此，我们需要把这两个贡献相加，得到 $g(x)$ 中 $x^j$ 的系数，即 $g[j + 1]$。这个系数的初始值为 $0$，每次递推时先加上原来的值，再加上 $g[j] \cdot t$ 即可更新。
    最终，当 $i$ 循环 $k$ 次后，$g$ 数组中存储的就是 $g(x)$ 的各项系数。具体来说，$g[x]$ 中存储的是 $g(x)$ 中 $x^{k-x}$ 的系数。
  • 将除法多项式 $D(x)$ 对多项式 $g(x)=(x-3)(x-3^2)…(x-3^k)$ 取模，并将余数存储在 $D(x)$ 中。其中，$D(x)$ 的各项系数存储在数组 $D$ 中，$g(x)$ 的各项系数存储在数组 $g$ 中，$k$ 是 $g(x)$ 的最高次幂次数，$mod$ 是一个取模变量。
    首先，将 $D(x)$ 的常数项系数初始化为 $n$，即 $D_0=n$。然后，将 $D(x)$ 的各项系数从数组 $d$ 中复制到数组 $D$ 中，通过循环实现： 
    1
    2
    for (int i = 1; i <= dnum; i++)
        D[i] = d[i - 1];
    其中，$dnum$ 表示 $d(x)$ 的最高次幂次数。
    接下来，对于 $D(x)$ 的每一项系数 $Di$，都通过 $g(x)$ 进行一次带余除法。具体来说，使用 $Di$ 乘以 $g(x)$ 的各项系数 $gj$，得到一个新的多项式 $Dix^jg(x)$，将其减去 $D(x)$ 的前 $i$ 项系数 $D0,D1,\ldots,D{i-1}$ 的线性组合，并将差存储在 $D{i+j}$ 中：
    1
    2
    for (int j = 1; j <= k; j++)
        D[i + j] = (D[i + j] - D[i] * g[j]) % mod;
    这里用到的余数公式是：
    $$
    f(x) \equiv g(x) \cdot q(x) + r(x) \pmod{m},
    $$
    其中 $f(x)$ 是被除多项式，$g(x)$ 是除数多项式，$q(x)$ 是商多项式，$r(x)$ 是余数多项式，$m$ 是取模变量。将这个公式代入上述代码，可以发现 $D(x)$ 对 $g(x)$ 取模后的余数 $r(x)$ 实际上就是 $D_ix^jg(x)$ 减去 $D(x)$ 的前 $i$ 项系数的值，再对 $m$ 取模。
    最后，将 $D(x)$ 的前 $i$ 项系数赋值为 $0$，以保证在之后的计算中不会重复使用：
    D[i] = 0;
    当两个循环都运行完毕后，$D(x)$ 中存储的就是 $D(x)$ 对 $g(x)$ 取模的余数。

期望得分100。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include<iostream>
#include<ctype.h>
#include<string>
#include<algorithm>
#define up 0
#define low 1
#define digit 2
const int mod = 929, N = 1e5 + 5;
int a[N], d[N], g[N], D[N];
using namespace std;
int check(char c) {
    if (isupper(c))
        return up;
    if (islower(c))
        return low;
    if(isdigit(c))
        return digit;
}

int main()
{
    ios::sync_with_stdio(false);
    int w, s;
    cin >> w >> s;
    string str;
    cin >> str;
    //校验码字数量
    int k;
    if (s == -1)
        k = 0;
    else
        k = 1 << (s + 1);

    int pre = up, nowindex = 0;
    for (int i = 0; i < str.length(); i++) {
        int now = check(str[i]);
        if (now == up) {
            if (pre == up)
                a[nowindex++]=str[i]-'A';
            else if (pre == low) {
                a[nowindex++] = 28;
                a[nowindex++] = 28;
                a[nowindex++] = str[i] - 'A';
            }
            else {
                a[nowindex++] = 28;
                a[nowindex++] = str[i] - 'A';
            }
        }
        else if (now == low) {
            if (pre == up) {
                a[nowindex++] = 27;
                a[nowindex++] = str[i] - 'a';
            }
            else if (pre == low)
                a[nowindex++] = str[i] - 'a';
            else {
                a[nowindex++] = 27;
                a[nowindex++] = str[i] - 'a';
            }
        }
        else {
            if (pre == up) {
                a[nowindex++] = 28;
                a[nowindex++] = str[i] - '0';
            }
            else if (pre == low) {
                a[nowindex++] = 28;
                a[nowindex++] = str[i] - '0';
            }
            else
                a[nowindex++] = str[i] - '0';
        }
        pre = now;
    }
    if (nowindex % 2)
        a[nowindex++] = 29;
    //有效码字处理
    int dnum = 0;
    for (int i = 0; i < nowindex; i += 2)
        d[dnum++] = a[i] * 30 + a[i + 1];
    //填充码字
    while ((dnum + k + 1) % w)
        d[dnum++] = 900;

    int d_n = dnum + 1;		//长度码字
    //先处理g(x)系数
    int t = -3;
    g[0] = 1;
    for (int i = 0; i < k; i++, t = t * 3 % mod)
        for (int j = i; j >= 0; j--)
            g[j + 1] = (g[j + 1] + g[j] * t) % mod;
    //处理多项式d(x)系数
    D[0] = d_n;
    for (int i = 1; i < d_n; i++)
        D[i] = d[i - 1];
    //开始取余求r(x)系数
    for (int i = 0; i < d_n; i++)
        for (int j = k; j >= 0; j--) 
            D[i + j] = (D[i + j] - D[i] * g[j]) % mod;

    cout << d_n << "\n";
    for (int i = 0; i < dnum; i++)
        cout << d[i] << "\n";
    for (int i = d_n; i < d_n + k; i++)
        cout << (-D[i] % mod + mod) % mod << "\n";
    return 0;
}

题目 4：磁盘文件操作

题目描述：

定义一组可能互斥的程序操作，如写、删、恢复这些操作是互斥的。写操作只能写到被自己占用磁盘空间、删除只能目标空间全被自己占用、恢复则只能上次自己占用的；读取也读取自己占用的。
给定很多这样的操作，同时在一块共享的磁盘空间上进行运行，根据上面操作的定义，其操作结果成功与否。比如写成功到什么位置(-1 表示一个也没写入)，删除恢复成功与否(用 OK, FAIL 表示)。

题解：

解法一：

直接模拟。

  • 写入操作：从左往右依次执行，直到第一个不被自己占用的位置。除了第一个点就被其他程序占用以外，必然会写入。遇到自己占用，则覆盖。
  • 删除操作：同时整体进行，要求所有位置都被目前程序占用。要么全删，要么不做任何更改。
  • 恢复操作：同时整体进行，要求所有位置都不被占用，且上次占用程序为目前程序。要么全恢复，要么不做任何更改。遇到自己占用，则不做任何更改。
  • 读入操作：读取占用程序和数值，若未被占用，则输出 0 0。

可通过25％数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<bits/stdc++.h>
const int N = 5e6 + 5;
using namespace std;
struct Node
{
    int val;
    int pre;
    int id;
}node[N];

int main()
{
    int n, m, k;
    cin >> n >> m >> k;
    while (k--) {
        int op;
        cin >> op;
        int id, l, r, x, p;
        if (op == 0) {
            cin >> id >> l >> r >> x;
            int i = l;
            for (i = l; i <= r; i++) {
                if (node[i].id == 0 || node[i].id == id) {
                    node[i].val = x;
                    node[i].id = id;
                }
                else
                    break;
            }
            if (i == l)
                cout << -1 << endl;
            else
                cout << i - 1 << endl;
        }
        else if (op == 1) {
            cin >> id >> l >> r;
            int flag = 1;
            for(int i = l; i <= r; i++)
                if (node[i].id != id) {
                    flag = 0;
                    break;
                }
            if (!flag)
                cout << "FAIL" << endl;
            else {
                cout << "OK" << endl;
                for (int i = l; i <= r; i++) {
                    node[i].pre = id;
                    node[i].id = 0;
                }
            }
        }
        else if (op == 2) {
            cin >> id >> l >> r;
            int flag = 1;
            for(int i = l; i <= r; i++)
                if (node[i].id != 0 || node[i].pre != id) {
                    flag = 0;
                    break;
                }
            if (!flag)
                cout << "FAIL" << endl;
            else {
                cout << "OK" << endl;
                for (int i = l; i <= r; i++)
                    node[i].id = id;
            }
        }
        else {
            cin >> p;
            if (node[p].id == 0)
                cout << "0 0" << endl;
            else
                cout << node[p].id << " " << node[p].val << endl;
        }
    }
    return 0;
}

解法二：

离散化+线段树。
我们假设一个位置未被占用和被 $id$ 为 $0$ 的程序占用是等价的。

  • 写入操作：划分为找到写入右边界和直接写入两个操作。
    直接写入操作就是直接的线段树区间修改， 而划分操作需要知道该区间被占用的位置是否属于将要写入的 $id$。 不妨将这个量设为 $id1$。
  • 删除操作：划分为判断是否可删和直接删除两个操作。
    直接删除操作就是直接的线段树区间修改， 而判断是否可删需要知道该区间所有的位置是否属于将要写入的 $id$。 不妨将这个量设为 $id2$，注意 $id1$ 与 $id2$ 的区别——是否允许包含未被占用的程序。
  • 恢复操作：划分为判断是否可恢复和直接恢复两个操作。
    该操作与删除操作类似，不过需要注意的是判断时需要判断目前占用的 $id$ 和上次被占用的 $id$。
  • 读取操作：划分为查询占用程序 $id$ 和查询值两个操作。
    该操作是相对比较质朴的单点查询，当然也可以处理为区间。
    线段树

    需要维护的量：
  • 值 $val$：每个节点代表取值的多少，若左右子节点不同则设为一个不存在的值。因为我们是单点查询，所以不用担心查询到不存在的值的问题。
  • 被占用位置程序 $id1$：
    • 若左右子节点都未被占用，则该节点标记为未占用（0）；
    • 若左右子节点中存在不唯一节点，则该节点标记为不唯一（-1）；
    • 若左右子节点中一个节点未占用，则该节点标记为另一个非空节点的标记；
    • 若左右子节点都非空且相等，则该节点标记为任意一个子节点；
    • 若左右子节点都非空且不等，则该节点标记为不唯一；
  • 被占用位置程序 $id2$：为了方便进行讨论，将未被程序占用节点视为被 $id$ 为 $0$ 的程序占用。
    • 若左右子节点中存在不唯一节点，则该节点标记为不唯一。
    • 若左右子节点相等，则该节点标记为任意一个子节点；
    • 若左右子节点不等，则该节点标记为不唯一；
  • 上一次被占用程序 $lid$：与 $id2$ 相同。
    • 若左右子节点中存在不唯一节点，则该节点标记为不唯一。
    • 若左右子节点相等，则该节点标记为任意一个节点；
    • 若左右子节点不等，则该节点标记为不唯一；

ls 和 rs 是代表节点编号的变量。在这段代码中，通过位运算的方式将 o << 1 和 ls | 1 分别表示为左右孩子节点的编号。具体而言，ls = o << 1 表示将 o 左移一位，并将结果赋值给 ls；rs = ls | 1 表示将 ls 二进制最低位设置为 1 ，作为右孩子的编号。这样做的好处是可以避免直接写出具体的左右孩子编号，在二叉树结点数量变化时保证程序稳定性。

通过离散化解决空间问题。
时间复杂度 $O(klogk)$，期望得分$100$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
#include<bits/stdc++.h>

using namespace std;

const int maxn = 200010;
const int INF = 1e9 + 10;
int n, m, k;
#define ls o << 1
#define rs ls | 1

struct treenode {
    // 当前节点的值，若不唯一则为 INF；lazy 为 INF 表示无延迟更新
    int val, lazy_val;
    // 当前占用 id，若存在除 0 以外两种 id 则为 -1；lazy 为 -1 表示无延迟更新
    int id1, lazy_id1;
    // 当前占用 id，若存在两种 id 则为 -1；lazy 为 -1 表示无延迟更新
    int id2, lazy_id2;
    // 上次占用 id，若存在两种 id 则为 -1；lazy 为 -1表示无延迟更新
    int lid, lazy_lid;
} tree[maxn << 5];

void pushup(int o) {
    // 线段树上传操作，合并左右子树结果 
    // val 的合并
    tree[o].val = (tree[ls].val == tree[rs].val) ? tree[ls].val : INF;
    // id1 的合并
    if (tree[ls].id1 == -1 || tree[rs].id1 == -1)//存在不唯一
        tree[o].id1 = -1;
    else if (tree[ls].id1 == tree[rs].id1) //子节点相同
        tree[o].id1 = tree[ls].id1;
    else if (tree[ls].id1 == 0)   //左节点未占用
        tree[o].id1 = tree[rs].id1;
    else if (tree[rs].id1 == 0)   //右节点未占用
        tree[o].id1 = tree[ls].id1;
    else                          //左右节点占用但不同
        tree[o].id1 = -1;
    // id2 的合并
    if (tree[ls].id2 == -1 || tree[rs].id2 == -1)//存在不唯一
        tree[o].id2 = -1;
    else if (tree[ls].id2 == tree[rs].id2)       //子节点相同
        tree[o].id2 = tree[ls].id2;
    else                                         //子节点不同
        tree[o].id2 = -1;
    // lid 的合并
    if (tree[ls].lid == -1 || tree[rs].lid == -1)
        tree[o].lid = -1;
    else if (tree[ls].lid == tree[rs].lid)
        tree[o].lid = tree[ls].lid;
    else
        tree[o].lid = -1;
}

void pushdown(int o) {
    // 线段树标记下传操作
    if (tree[o].lazy_val != INF) {
        tree[ls].val = tree[rs].val = tree[o].lazy_val;
        tree[ls].lazy_val = tree[rs].lazy_val = tree[o].lazy_val;
        tree[o].lazy_val = INF;
    }
    if (tree[o].lazy_id1 != -1) {
        tree[ls].id1 = tree[rs].id1 = tree[o].lazy_id1;
        tree[ls].lazy_id1 = tree[rs].lazy_id1 = tree[o].lazy_id1;
        tree[o].lazy_id1 = -1;
    }
    if (tree[o].lazy_id2 != -1) {
        tree[ls].id2 = tree[rs].id2 = tree[o].lazy_id2;
        tree[ls].lazy_id2 = tree[rs].lazy_id2 = tree[o].lazy_id2;
        tree[o].lazy_id2 = -1;
    }
    if (tree[o].lazy_lid != -1) {
        tree[ls].lid = tree[rs].lid = tree[o].lazy_lid;
        tree[ls].lazy_lid = tree[rs].lazy_lid = tree[o].lazy_lid;
        tree[o].lazy_lid = -1;
    }
}

void build(int o, int l, int r) {
    // 线段树初始化建树
    if (l == r) {
        tree[o].val = 0;
        tree[o].lazy_val = INF;
        tree[o].id1 = tree[o].id2 = tree[o].lid = 0;
        tree[o].lazy_id1 = tree[o].lazy_id2 = tree[o].lazy_lid = -1;
        return;
    }
    int mid = (l + r) >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
    tree[o].lazy_val = INF;
    pushup(o);
}

#define ALLOK -2
int find_right(int o, int l, int r, int ql, int qid) {
    // 操作一中，固定左端点，寻找右端点可能的最大值 
    // 这里没有考虑和右端点的比较，直接寻找了最大的可能值
    pushdown(o);
    if (r < ql || tree[o].id1 == qid || tree[o].id1 == 0)
        return ALLOK;  //全符合条件
    else if (tree[o].id2 != -1)
        return l - 1;  //不符合条件。返回该区域右边第一个
    else {
        // 需要寻找确切位置 
        // 先查找左区间，如果左区间全满足则再寻找右区间
        int mid = (l + r) >> 1;
        int leftPart = (ql <= mid) ? find_right(ls, l, mid, ql, qid) : ALLOK;
        return (leftPart == ALLOK) ? find_right(rs, mid + 1, r, ql, qid) : leftPart;
    }
}
#undef ALLOK

void modify_val(int o, int l, int r, int ql, int qr, int val, int id, bool ignoreLid = false) {
    // 若 val = INF 代表不需要对 val 进行处理 
    // 若 ignoreLid = true 则不对 lid 进行更改
    if (l >= ql && r <= qr) {
        if (val != INF)
            tree[o].val = tree[o].lazy_val = val;
        tree[o].id1 = tree[o].lazy_id1 = id;
        tree[o].id2 = tree[o].lazy_id2 = id;
        if (!ignoreLid)
            tree[o].lid = tree[o].lazy_lid = id;
        return;
    }
    pushdown(o);
    int mid = (l + r) >> 1;
    if (ql <= mid)
        modify_val(ls, l, mid, ql, qr, val, id, ignoreLid);
    if (qr > mid)
        modify_val(rs, mid + 1, r, ql, qr, val, id, ignoreLid);
    pushup(o);
}

bool is_same_id(int o, int l, int r, int ql, int qr, int id, bool isRecover = false) {
    // 判断该区域 id 和 lid 是否满足条件
    if (l >= ql && r <= qr) {
        if (isRecover)    // 检查 id = 0 且 lid = id
            return (tree[o].id2 == 0 && tree[o].lid == id);
        else              // 检查 id = id
            return (tree[o].id2 == id);
    }
    pushdown(o);
    int mid = (l + r) >> 1;
    bool isSame = true;
    if (ql <= mid)
        isSame = isSame && is_same_id(ls, l, mid, ql, qr, id, isRecover);
    if (qr > mid && isSame)
        isSame = isSame && is_same_id(rs, mid + 1, r, ql, qr, id, isRecover);
    return isSame;
}

int query_val(int o, int l, int r, int p) {
    // 线段树单点求值：val
    if (p >= l && p <= r && tree[o].val != INF)
        return tree[o].val;
    pushdown(o);
    int mid = (l + r) >> 1;
    if (p <= mid)
        return query_val(ls, l, mid, p);
    else
        return query_val(rs, mid + 1, r, p);
}

int query_id(int o, int l, int r, int p) {
    // 线段树单点求值：id2
    if (p >= l && p <= r && tree[o].id2 != -1)
        return tree[o].id2;
    pushdown(o);
    int mid = (l + r) >> 1;
    if (p <= mid)
        return query_id(ls, l, mid, p);
    else
        return query_id(rs, mid + 1, r, p);
}

#undef ls
#undef rs

struct instruction {
    int opt, id, l, r, x;
} inst[maxn];
// numList 存储所有可能出现的数，totnum 表示个数
int numList[maxn << 2], totnum;
void discretization() {
    // 离散化操作
    sort(numList + 1, numList + 1 + totnum);
    totnum = unique(numList + 1, numList + 1 + totnum) - numList - 1;
    m = totnum;
    for (int i = 1; i <= k; ++i) {
        if (inst[i].opt == 0 || inst[i].opt == 1 || inst[i].opt == 2) {
            inst[i].l = lower_bound(numList + 1, numList + 1 + totnum, inst[i].l) - numList;
            inst[i].r = lower_bound(numList + 1, numList + 1 + totnum, inst[i].r) - numList;
        }
        else
            inst[i].x = lower_bound(numList + 1, numList + 1 + totnum, inst[i].x) - numList;
    }
}

int main() 
{
    scanf("%d%d%d", &n, &m, &k);
    numList[++totnum] = 1;
    numList[++totnum] = m;
    for (int i = 1; i <= k; ++i) {
        scanf("%d", &inst[i].opt);
        if (inst[i].opt == 0) {
            scanf("%d%d%d%d", &inst[i].id, &inst[i].l, &inst[i].r, &inst[i].x);
            numList[++totnum] = inst[i].l;
            numList[++totnum] = inst[i].r;
            // 注意边界问题，为了方便这里把交界处两点分开了，下同
            if (inst[i].l != 1)
                numList[++totnum] = inst[i].l - 1;
            if (inst[i].r != m)
                numList[++totnum] = inst[i].r + 1;
        }
        else if (inst[i].opt == 1) {
            scanf("%d%d%d", &inst[i].id, &inst[i].l, &inst[i].r);
            numList[++totnum] = inst[i].l;
            numList[++totnum] = inst[i].r;
            if (inst[i].l != 1)
                numList[++totnum] = inst[i].l - 1;
            if (inst[i].r != m)
                numList[++totnum] = inst[i].r + 1;
        }
        else if (inst[i].opt == 2) {
            scanf("%d%d%d", &inst[i].id, &inst[i].l, &inst[i].r);
            numList[++totnum] = inst[i].l;
            numList[++totnum] = inst[i].r;
            if (inst[i].l != 1)
                numList[++totnum] = inst[i].l - 1;
            if (inst[i].r != m)
                numList[++totnum] = inst[i].r + 1;
        }
        else
            scanf("%d", &inst[i].x);
            // 对于查询的数，不需要进行离散化，查找第一个比它大的数即可
    }
    // 离散化处理
    discretization();
    // 线段树初始化建树
    build(1, 1, m);
    // 进行操作
    for (int i = 1; i <= k; ++i) {
        if (inst[i].opt == 0) {
            // 写入操作：先求得范围，再进行填充
            int r = find_right(1, 1, m, inst[i].l, inst[i].id);
            if (r == -2)
                // r = -2 代表全部满足
                r = inst[i].r;
            else
                r = min(r, inst[i].r);
            if (inst[i].l <= r) {
                printf("%d\n", numList[r]); // 注意返回离散化前的值
                modify_val(1, 1, m, inst[i].l, r, inst[i].x, inst[i].id);
            }
            else
                printf("-1\n");
        }
        else if (inst[i].opt == 1) {
            // 删除操作：先判断是否可行，之后执行
            if (is_same_id(1, 1, m, inst[i].l, inst[i].r, inst[i].id)) {
                printf("OK\n");
                modify_val(1, 1, m, inst[i].l, inst[i].r, INF, 0, true);
            }
            else
                printf("FAIL\n");
        }
        else if (inst[i].opt == 2) {
            // 恢复操作：先判断是否可行，之后执行
            if (is_same_id(1, 1, m, inst[i].l, inst[i].r, inst[i].id, true)) {
                printf("OK\n");
                modify_val(1, 1, m, inst[i].l, inst[i].r, INF, inst[i].id, true);
            }
            else
                printf("FAIL\n");
        }
        else if (inst[i].opt == 3) {
            // 读取操作：分别读取 id 和 val
            int id = query_id(1, 1, m, inst[i].x);
            int val = query_val(1, 1, m, inst[i].x);
            if (id == 0)
                printf("0 0\n");
            else
                printf("%d %d\n", id, val);
        }
    }
    return 0;
}

题目 5：极差路径

题目描述：

给定一颗树，定义一条路径是被推荐的，当且仅当：
$$min(x,y)-k_1≤minP(x,y)≤maxP(x,y)≤max(x,y)+k_2$$
其中，$minP(x,y)$表示从 $x$ 到 $y$ 的简单路径上的编号最小值，$maxP(x,y)$表示从 $x$ 到 $y$ 的简单路径上的编号最大值。
$(x,y)$ 和 $(y,x)$ 被视为同一条路径。
求被推荐的路径条数。
$1≤n≤5×10^5，0≤k_1，k_2≤n$

题解：

解法一：

dfs暴力搜索。
时间复杂度 $O(n^3)$，期望得分12。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>
using namespace std;

const int N = 5e5 + 10;

int n, k1, k2;
vector<int> g[N];
vector<int> v;
int vis[N];
set<pair<int, int>> res;

void dfs(int x, vector<int>& v, int y)
{
    int minnum = min(x, y) - k1;
    int maxnum = max(x, y) + k2;
    int minp = *(min_element(v.begin(), v.end()));
    int maxp = *(max_element(v.begin(), v.end()));
    if (minnum <= minp && minp <= maxp && maxp <= maxnum)
    {
        int a = x, b = y;
        if (a > b) swap(a, b);
        pair<int, int> p = make_pair(a, b);
        res.insert(p);
    }
    for (int i = 0; i < g[y].size(); i++)
    {
        int temp = g[y][i];
        if (vis[temp] == 0)
        {
            v.push_back(temp);
            vis[temp] = 1;
            dfs(x, v, temp);
            v.pop_back();
            vis[temp] = 0;
        }
    }
}

int main()
{
    cin >> n >> k1 >> k2;
    for (int i = 0; i < n - 1; i++)
    {
        int x, y;
        cin >> x >> y;
        g[x].push_back(y);
        g[y].push_back(x);
    }
    for (int i = 1; i <= n; i++)
    {
        memset(vis, 0, sizeof(vis));
        v.clear();
        v.push_back(i);
        vis[i] = 1;
        dfs(i, v, i);
    }
    cout << res.size() << endl;
    return 0;
}

解法二：

点分治+三位数点。
定义一个点的权值为它的最大子树的大小。
以重心为根，最大子树的大小，必然不大于树中总点数的一半。
每次操作统计所有与重心相连接的路径，再将重心消除，形成一个森林，再递归操作下去。

假设当前处理的根节点为 $u$，从 $u$ 开始dfs一遍得到从 $u$ 到各点路径的$min$和$max$，用三元组$(v,minv,maxv)$表示。
合法路径的条数满足$$v_1<v_2，
v_1-k_1≤min(minv_1​,minv_2​),max(maxv_1​,maxv_2​)≤v_2​+k_2$$​的三元组$(v_1​,minv_1​,maxv_1​),(v_2​,minv_2​,maxv_2$)的对数。

为降低时间复杂度，选择可持久化线段树。
按照点的编号将三元组排序后，按编号从小到大依次处理。
$v_1​−k_1​≤min(minv_1​,minv_2​)$可以拆分成 $v_1​−k_1​≤minv_1$ ​和 $v_1​−k_1​≤minv_2$​，前面的式子可以直接判断。
同样的，将 $max(maxv_1​,maxv_2​)≤v_2​+k_2$ ​拆分成 $maxv_1​≤v_2​+k_2$ ​和 $maxv_2​≤v_2​+k_2$​，后面的式子可以直接判断。

处理 $v_1​−k_1​≤minv_2$​ 和 $maxv_1​≤v_2​+k_2$ :
在 $root[v_1​−k_1​]$ 线段树的 $maxv_1$ ​位置进行$+1$操作。然后枚举到 $v_2$ ​时，对应的以 $v_2$ ​为大端的路径条数就是 $root[minv_2​]$ 中区间 $1⋯v_2​+k_2$ ​的和。

时间复杂度 $O(nlogn)$，期望得分$100$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
#include <bits/stdc++.h>
using namespace std;

const int maxn = 5e5 + 10;
const int INF = 1e9 + 10;
vector<int> g[maxn];
int S, Mx, K1, K2, n, root;
int sm[maxn], mxson[maxn], vis[maxn];
char buf[1 << 23], * p1 = buf, * p2 = buf, obuf[1 << 23], * O = obuf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)

inline int rd() 
{
    int x = 0, f = 1; 
    char ch = getchar();
    while (!isdigit(ch)) { 
        if (ch == '-') 
            f = -1; 
        ch = getchar(); 
    }
    while (isdigit(ch)) 
        x = x * 10 + (ch ^ 48), ch = getchar();
    return x * f;
}

void getrt(int u, int fa) 
{
    sm[u] = 1;
    mxson[u] = 0;
    for (int v : g[u]) if (!vis[v] && v != fa) {
        getrt(v, u);
        sm[u] += sm[v];
        mxson[u] = max(mxson[u], sm[v]);
    }
    mxson[u] = max(mxson[u], S - sm[u]);
    if (mxson[u] < Mx) {
        root = u;
        Mx = mxson[u];
    }
}

void get(int u, int fa, vector<int>& nodes, pair<int, int>* value, int mn, int mx) 
{
    nodes.push_back(u);
    value[u].first = mn;
    value[u].second = mx;
    for (int v : g[u]) if (!vis[v] && v != fa)
        get(v, u, nodes, value, min(mn, v), max(mx, v));
}

int rt[maxn], sz[maxn * 20], ch[maxn * 20][2], top = 0;
int newnode(int x) 
{
    sz[++top] = sz[x];
    ch[top][0] = ch[x][0];
    ch[top][1] = ch[x][1];
    return top;
}

void ins(int& rt, int l, int r, int val) 
{
    rt = newnode(rt);
    sz[rt]++;
    int t = rt;
    while (l < r) {
        int mid = l + r >> 1;
        if (val <= mid)
            ch[t][0] = newnode(ch[t][0]), t = ch[t][0], sz[t]++, r = mid;
        else
            ch[t][1] = newnode(ch[t][1]), t = ch[t][1], sz[t]++, l = mid + 1;
    }
}

int get(int rt, int l, int r, int x) 
{
    int cnt = 0;
    while (l < r) {
        int mid = l + r >> 1;
        if (x <= mid) 
            rt = ch[rt][0], r = mid;
        else 
            cnt += sz[ch[rt][0]], rt = ch[rt][1], l = mid + 1;
    }
    cnt += sz[rt];
    return cnt;
}

long long solve(int v, int mn, int mx) 
{
    vector<int> nodes;
    static int w[maxn];
    static pair<int, int> value[maxn];
    get(v, 0, nodes, value, min(mn, v), max(mx, v));
    for (int i = 0; i < nodes.size(); i++) 
        w[i] = nodes[i];
    sort(w, w + nodes.size());
    long long cnt = 0;
    top = 0;
    rt[0] = 0;
    for (int i = 0; i < nodes.size(); i++) {
        auto p = value[w[i]];
        if (i) 
            rt[i] = rt[i - 1];
        if (w[i] - K1 <= p.first) 
            ins(rt[i], 1, n, p.second);
        if (w[i] + K2 >= p.second) {
            int nv = p.first + K1;
            int l = -1, r = nodes.size() - 1;
            while (l < r) {
                int mid = l + r + 1 >> 1;
                if (w[mid] > nv) 
                    r = mid - 1; 
                else 
                    l = mid;
            }
            int pos = min(l, i);
            if (pos >= 0)
                cnt += get(rt[pos], 1, n, w[i] + K2);
        }
    }
    return cnt;
}

long long ans = 0;
void Divide(int rt) 
{
    ans += solve(rt, INF, 0);
    vis[rt] = 1;
    for (int v : g[rt]) if (!vis[v]) {
        ans -= solve(v, rt, rt);
        S = sm[v];
        root = 0;
        Mx = INF;
        getrt(v, 0);
        Divide(root);
    }
}

int main() 
{
    n = rd();
    K1 = rd();
    K2 = rd();
    for (int i = 1; i < n; i++) {
        int u, v;
        u = rd();
        v = rd();
        g[u].push_back(v);
        g[v].push_back(u);
    }
    Mx = INF;
    S = n;
    getrt(1, 0);
    Divide(root);
    cout << ans << endl;
    return 0;
}
赏

谢谢你请我吃糖果

支付宝
微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

北京邮电大学计算机科学与技术在读<br>联系:WilliamZH29@outlook.com