第21次CCFCSP题4解题报告

2024-08-14

1.5k字 | 预计阅读时长: 6min

阅读量: 次

本次报告撰写人：WilliamZH
题目：202012-4，第21次CCFCSP
使用语言：C++

202012-4 食材运输

题目描述：

$N$ 个酒店，由 $N-1$ 条双向道路构成一棵树，不同道路对应不同通行时间。
$K$ 种食材对应 $K$ 辆车，$M$ 个检查点作为车辆起点。
求所有酒店的等待时间的最大值的最小值。
输入格式：
第一行 $N,M,K$；接下来 $N$ 行，每行 $K$ 个数（$1$ 表示需要对应食材，$0$ 表示不需要）；接下来 $N-1$ 行，每行 $3$ 个整数 $u,v,w$（通行时间为 $w$ 的双向道路连接 $u$ 和 $v$）。
输出格式：
输出一个整数，表示在你的方案中，所有酒店的等待时间的最大值。
$N\leq10^2,M\leq K\leq10$.

题解：

主要思路：先预处理所有数据，然后进行动态规划，最后二分查找来尝试不同的时间（通过时间选择方案）

存储所有数据：
用位图表示来处理各个酒店所需要的食材，用 $01$ 表示各食材的需求情况：第 $i$ 位表示对第 $i$ 号食材的需求（$1$ 表示需要，$0$ 则不需要），从而将所有食材压缩到一个整数上，该整数表示该点对所有食材的需求情况。
对于每个节点存储的信息（指向酒店 $v$，与 $v$ 之间道路时长 $w$），通过 $vector$ 结构进行添加信息，因为是双向道路，所以需要同时对 $u，v$ 都进行添加。
$intitial$ 函数部分：
计算从酒店 $i$ 出发，配送食材 $j$ 的最大等待时间。
在进行 $dfs$ 之前，用 $bool$ 数组标记出哪些酒店需要该食材；需要注意的是，在 $dfs$ 中，某些必经点（下图的蓝色节点）也要标记出来。（每个标记循环前需要将该数组置零）
$dfs$ 部分：提供当前酒店号 $u$，和来源酒店号 $pre$。（当前节点和上一个节点）
求解最大等待时间算法解释：
其实只分为两种情况：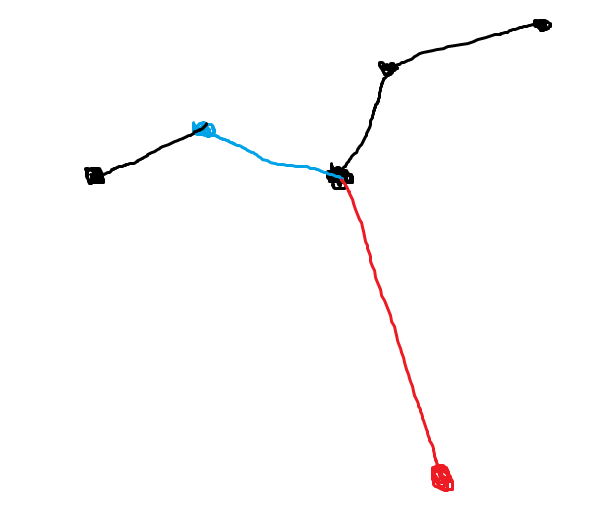
1. 该节点 $\to$ 不需要食材的节点（蓝色路径） $\to$ 需要食材的节点（黑色路径）
2. 该节点 $\to$ 需要食材的节点（黑色路径）
  则总路径应为其中一条子路径走一次，其余子路径去并返回。即 $maxtime=onetime*2-maxn$，其中 $onetime$ 表示全部的单程路径，$maxn$ 表示途中红色的最长的路径。
$work$ 函数部分：
1. $M==K$
  先遍历各食材最小解，从最小解里选出最大值。
2. $M<K$
  备忘录 dp+二分查找
  用位图标记某酒店是否适合配送每一个食材（时长<mid 表示适合）
  dp 方程：
  第 j 个检查点的配送情况=第 $j-1$ 个检查点情况叠加酒店 i 的配送情况

#include<iostream>
#include<vector>
#include<algorithm>
#include<string.h>
using namespace std;
int N, M, K;
int foodbit[101];			//位图表示
int waitmax[101][11];		//记录从酒店i出发配送食材j的最大等待时间
bool passneed[101];			//标记是否需要经过该酒店
int onetime;				//配送所有酒店的单程时间
int maxnn = 0, minnn = 0;	//记录二分时的左右边界
bool dp[11][1 << 10];		//表示是否可送达K种食材的配送组合
int flag[101];				//位图标记某酒店是否适合配送每一个食材
struct node {
    int v, w;
    node(int v, int w):v(v),w(w){}
};
vector<node> map[101];

int dfs(int u, int pre) {
    int ret = 0;
    //深度优先遍历u为顶点的所有路径
    for (const auto& x : map[u]) {
        int v = x.v;
        int w = x.w;
        if (v == pre)
            continue;
        int re = dfs(v, u);
        //处理必经点（不需要食材但子节点需要且必经过该节点）
        if (passneed[v]) {
            passneed[u] = true;
            onetime += w;
            ret = max(ret, re + w);
        }
    }
    return ret;
}

void initial() {
    for (int i = 1; i <= N; i++)
        for (int j = 0; j < K; j++) {
            //事先标记
            memset(passneed, 0, sizeof(passneed));
            for (int k = 1; k <= N; k++)
                if (foodbit[k] >> j & 1)
                    passneed[k] = true;
            //初始化单程时间
            onetime = 0;
            //从第i个酒店开始的情况下，找到最长的路径
            int maxn = dfs(i, -1);
            //其他路径去并返回，最长路径只走一次不返回
            waitmax[i][j] = onetime * 2 - maxn;
            //为二分查找的边界做准备
            if (waitmax[i][j] > maxnn)
                maxnn = waitmax[i][j];
            else if (waitmax[i][j] < minnn)
                minnn = waitmax[i][j];
        }
}

bool judge(int mid) {
    memset(flag, 0, sizeof(flag));
    memset(dp, 0, sizeof(dp));
    //位图标记酒店i是否适合配送食材j
    for (int i = 1; i <= N; i++)
        for (int j = 0; j < K; j++)
            if (waitmax[i][j] <= mid)
                flag[i] |= 1 << j;

    dp[0][0] = true;
    //遍历酒店，以酒店i为出发点
    for (int i = 1; i <= N; i++) {
        //遍历检查点，酒店i在j个检查点时的配送情况
        for (int j = 1; j <= M; j++)
            for (int k = 0; k < (1 << K); k++)
                dp[j][k | flag[i]] |= dp[j - 1][k];
        if (dp[M][(1 << K) - 1])
            return true;
    }
    return dp[M][(1 << K) - 1];
}

void work() {
    if (M == K) {
        int ansmax = -1;
        for (int j = 0; j < K; j++) {
            int foodmin = maxnn;
            for (int i = 1; i <= N; i++)
                if (waitmax[i][j] < foodmin)
                    foodmin = waitmax[i][j];
            ansmax = max(ansmax, foodmin);
        }
        cout << ansmax << "\n";
        return;
    }
    int l = minnn, r = maxnn, ans = 0;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (judge(mid)) {
            r = mid - 1;
            ans = mid;
        }
        else
            l = mid + 1;
    }
    cout << ans << "\n";
    return;
}

int main()
{
    ios::sync_with_stdio(false);
    //输入
    cin >> N >> M >> K;
    for (int i = 1; i <= N; i++)
        for (int j = 0; j < K; j++) {
            int temp;
            cin >> temp;
            if (temp)
                foodbit[i] |= (1 << j);
        }
    for (int i = 1; i < N; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        map[u].emplace_back(v, w);
        map[v].emplace_back(u, w);
    }
    //预处理
    initial();
    //计算结果
    work();
    return 0;
}